Computación Cuántica¶
Preliminares¶
Este material presenta una introducción a la algorítmica básica en el cómputo cuántico, así como conceptos periféricos, utilizando la interfaz de programación contenida en el paquete Yao en Julia.
La computacón cuántica es un área mucho más extensa que solo lo que se discutirá aquí, e incluso actualmente no se tiene un panorama consensuado de lo que deberían ser las capas, arquitectura o flujo de la computación cuántica, comenzando desde su implementación física hasta cualquier aplicación que haga uso abstracto de dicha implementación.
No obstante, para ejemplificar una posible visión, mostramos la siguiente imagen:

Aquí podemos apreciar que la algorítmica es una abstracción de las posibles implementaciones físicas que pueden existir y además es resultado de un conjunto de asunciones teóricas que se deben procurar garantizar en las implementaciones mediante cuidados de la capa 2: Virtual (corrección de error, desacoplamiento dinámico, ciclo de control-retroalimentación del sistema, etc.)
Abstracción a nivel de circuito¶
Diseño de un circuito¶
En la algorítmica del cómputo cuántico trabajamos con los siguientes objetos abstractos (que pueden ser implementados de diversas maneras físicamente):
Registros de qubits
compuertas lógicas cuántica
Aparatos de medición
Ligaduras de control
Para proveer un ejemplo de un diagrama que contenga todos estos elementos considere el siguiente:

Tenemos un registro de qubits que consiste de los qubits \(\{Q_0, Q_1, Q_2, Q_3\}\). Éstos están todos en el estado \(|0\rangle\), como suele ser común para muchos algoritmos cuánticos.
Los cuadrados, etiquetado uno con una X y otros 7 con H, son ejemplos de compuertas lógicas. Respectivamente se les conoce como compuerta X de Pauli y compuerta de Hadamard.
Éstas, matemáticamente hablando, son operadores unitarios de los cuales, como es bien conocido, tenemos infinitos para cualquier espacio de Hilbert no trivial con el que trabajemos en nuestro sistema cuántico.
No obstante, elegimos darle nombres a éstas por permitir cálculos limpios en ciertas elecciones de base importantes que podemos realizar en el espacio de Hilbert. Las lineas verticales que conectan algunos de los qubits y poseen un nodo con \(\oplus\) y otro relleno son otro ejemplo de compuerta lógica, aunque más compleja
Éstas son compuertas de control que pueden influir en el estado de un qubit en base al estado de otro. Estas son un ejemplo de lo que llamamos compuertas compuestas que, matemáticamente, son operadores del espacio producto de los espacios de estado de los qubits involucrados.
Finalmente, al final de la linea de acción de cada uno de los qubits tenemos un elemento de diagrama que simboliza un aparato de medición. Éstos son necesarios para obtener la información contenida en los estados del registro, considerado el output o salida del algoritmo cuántico que este circuito representa.
Registro de estados¶
Registros completamente activos¶
Comencemos creando algunos registros. Primero cargamos el paquete Yao:
using Pkg; Pkg.activate("."); using Yao
Activating environment at `~/work/Intro-Julia-2021/Intro-Julia-2021/Project.toml`
Podemos crear el registro del diagrama de arriba utilizando la función zero_state que nos otorga con facilidad este común registro de cualquier tamaño:
zero_state(4)
ArrayReg{1, Complex{Float64}, Array...}
active qubits: 4/4
Como la naturaleza de la medición que obtenemos de los qubits es inevitablemente probabilística, a veces es deseado tener un número de batches o lotes que representan varias realizaciones del mismo circuito para obtener estadísticas.
En este siguiente comando creamos 5 lotes de un registro de 3 qubits, todos en el estado \(|0\rangle\).
zero_state(3, nbatch = 5)
ArrayReg{5, Complex{Float64}, Transpose...}
active qubits: 3/3
Podemos también construir un registro a partir de una cadena de bits que representa en análogo clásico del estado cuántico (respecto a alguna base):
product_state(bit"101")
ArrayReg{1, Complex{Float64}, Array...}
active qubits: 3/3
Para cualquier registro podemos extraer el estado explícito como arreglo de números complejos de la siguiente manera:
product_state(bit"101").state
8×1 Array{Complex{Float64},2}:
0.0 + 0.0im
0.0 + 0.0im
0.0 + 0.0im
0.0 + 0.0im
0.0 + 0.0im
1.0 + 0.0im
0.0 + 0.0im
0.0 + 0.0im
Notemos que este vector no tendrá \(3\) elementos correspondiendo a los 3 digitos de la cadena de bits, si no que tendremos \(8 = 2^3\).
Por supuesto podemos también construir más de un lote, y también cambiar el tipo de número complejo utilizando para guardar en memoria el estado:
product_state(ComplexF32, bit"111", nbatch = 3)
ArrayReg{3, Complex{Float32}, Transpose...}
active qubits: 3/3
product_state(ComplexF32, bit"111", nbatch = 3).state
8×3 LinearAlgebra.Transpose{Complex{Float32},Array{Complex{Float32},2}}:
0.0+0.0im 0.0+0.0im 0.0+0.0im
0.0+0.0im 0.0+0.0im 0.0+0.0im
0.0+0.0im 0.0+0.0im 0.0+0.0im
0.0+0.0im 0.0+0.0im 0.0+0.0im
0.0+0.0im 0.0+0.0im 0.0+0.0im
0.0+0.0im 0.0+0.0im 0.0+0.0im
0.0+0.0im 0.0+0.0im 0.0+0.0im
1.0+0.0im 1.0+0.0im 1.0+0.0im
A veces no necesitamos especificar el estado explícito, y queremos en su lugar generar un estado aleatorio (basándonos en una distribución binormal estándar) que nos permita poner a prueba cierto circuito independiente de sus entradas:
rand_state(2)
ArrayReg{1, Complex{Float64}, Array...}
active qubits: 2/2
rand_state(2).state ## Estado de 2 qubits tiene 2^2 = 4 entradas.
4×1 Array{Complex{Float64},2}:
-0.1896368759138612 - 0.3776013714095296im
0.3400142935772096 + 0.2570937642403422im
0.5366139754527408 + 0.01986814666971504im
-0.5621744017765454 - 0.18803929440171613im
Otro registro comúnmente utilizado es el registro de estados uniformes:
uniform_state(4).state
16×1 Array{Complex{Float64},2}:
0.25 + 0.0im
0.25 + 0.0im
0.25 + 0.0im
0.25 + 0.0im
0.25 + 0.0im
0.25 + 0.0im
0.25 + 0.0im
0.25 + 0.0im
0.25 + 0.0im
0.25 + 0.0im
0.25 + 0.0im
0.25 + 0.0im
0.25 + 0.0im
0.25 + 0.0im
0.25 + 0.0im
0.25 + 0.0im
Estos tienen la forma: \(\frac{1}{n} \sum_k |k\rangle\) y pueden ser similarmente obtenidos tras aplicar una compuerta de hadamar multidimensional a un registro de puros estados \(|0\rangle\) (es decir, una compuerta de hadamard sencilla por cada qubit).
Finalmente, mostramos que cualquier registro puede ser representado en su forma hiperbólica, es decir, como elemento de un espacio tensorial general.
hypercubic(uniform_state(4))
2×2×2×2×1 Array{Complex{Float64},5}:
[:, :, 1, 1, 1] =
0.25+0.0im 0.25+0.0im
0.25+0.0im 0.25+0.0im
[:, :, 2, 1, 1] =
0.25+0.0im 0.25+0.0im
0.25+0.0im 0.25+0.0im
[:, :, 1, 2, 1] =
0.25+0.0im 0.25+0.0im
0.25+0.0im 0.25+0.0im
[:, :, 2, 2, 1] =
0.25+0.0im 0.25+0.0im
0.25+0.0im 0.25+0.0im
Comparando dimensiones:
uniform_state(4) |> state |> size
(16, 1)
hypercubic(uniform_state(4)) |> size
(2, 2, 2, 2, 1)
El último muestra cómo el elemento del espacio vectorial de dimension 16 se entiende como un elemento de un espacio vectorial generado a partir de productos tensoriales de 4 espacios vectoriales de dimensión 2 (es decir, los espacios asociados a cada qubit individual).
Registros enfocados¶
En la práctica, no todos los qubits presentes en el sistema que consideramos el “computador cuántico” son utilizados para realizar operaciones. Muchos están presentes para asistir a procedimientos de corrección de error o flujo de control entre componentes, pero éstos no son menos importantes de preservar bajo coherencia cuántica.
Estos qubits de ambiente, no obstante, deben ser considerados explícitamente ya que afectan el estado general del registro y Yao provee una interfaz para hacer eso. Considere el siguiente registro
zero_state(5) |> focus!(1,4,5)
ArrayReg{1, Complex{Float64}, Array...}
active qubits: 3/5
Notemos que el resultado nos muestra solmente \(3\) de los \(5\) qubits como qubits activo. Estos qubits activos son lo que conocemos como qubits de sistema y son sobre lso que operaremos. El resto solo funcionan como ambiente. El estado general del registro sigue siendo el mismo que si todos fueran activos:
(zero_state(5) |> focus!(1,4,5)).state
8×4 Array{Complex{Float64},2}:
1.0+0.0im 0.0+0.0im 0.0+0.0im 0.0+0.0im
0.0+0.0im 0.0+0.0im 0.0+0.0im 0.0+0.0im
0.0+0.0im 0.0+0.0im 0.0+0.0im 0.0+0.0im
0.0+0.0im 0.0+0.0im 0.0+0.0im 0.0+0.0im
0.0+0.0im 0.0+0.0im 0.0+0.0im 0.0+0.0im
0.0+0.0im 0.0+0.0im 0.0+0.0im 0.0+0.0im
0.0+0.0im 0.0+0.0im 0.0+0.0im 0.0+0.0im
0.0+0.0im 0.0+0.0im 0.0+0.0im 0.0+0.0im
Pero en cualquier momento somos capaces de encontrar el número de qubits de sistema y qubits de ambiente de un registro dado:
ψ₁ = zero_state(5) |> focus!(1,4,5)
ArrayReg{1, Complex{Float64}, Array...}
active qubits: 3/5
nqubits(ψ₁), nactive(ψ₁), nremain(ψ₁)
(5, 3, 2)
Si queremos “relajar” los qubits de ambiente hacia un estado de control con el cual podamos operar, se puede utilizar el comando relax! de las siguientes formas:
ψ₁ |> relax!()
ArrayReg{1, Complex{Float64}, Array...}
active qubits: 5/5
relax!(ψ₁)
ArrayReg{1, Complex{Float64}, Array...}
active qubits: 5/5
relax!(ψ₁, to_nactive = 4)
ArrayReg{1, Complex{Float64}, Array...}
active qubits: 4/5
En el último llamado se muestra que podemos controlar el número de qubits del sistema con el que queremos terminar. Note que no elegimos los índices de “cuales” qubits activar (recordando que antes estaban activos los de índice 5, 3, y 2).
Esto es porque el índice de cierto qubit es un ordemamiento arbitrario: No importa si consideramos que el registro activo consiste de los qubits que originalmente llamamos \(\{5,2,3\}\) o de otros, pues esas etiquetas originales fueron arbitrarias para la física.
Aritmética de registros¶
Podemos operar con la aritmética esperada sobre nuestros registros mientras sea teóricamente válida la operación.
begin
ψ₂ = rand_state(5)
ψ₃ = rand_state(5)
end
ArrayReg{1, Complex{Float64}, Array...}
active qubits: 5/5
(0.3ψ₂ + 2ψ₃)/2
ArrayReg{1, Complex{Float64}, Array...}
active qubits: 5/5
(0.3ψ₂ + 2ψ₃)/2 |> state
32×1 Array{Complex{Float64},2}:
-0.016833451080093258 - 0.3008434221386917im
-0.24783133228903245 + 0.17980515085884655im
-0.009447713460595305 + 0.08937467711404697im
0.05963471646562052 + 0.24867815359548484im
0.11580472467834067 - 0.036431472178291915im
0.029254554388538745 + 0.08486879501206077im
-0.02364868292805669 + 0.12862605157316842im
0.004506201005053704 + 0.08418206209034758im
-0.056105273283056846 - 0.0009758546017973949im
0.035019769098548384 + 0.02633126344717432im
0.237515109130529 + 0.2034068876811752im
-0.2156108156813425 + 0.18829928869087037im
-0.20440015376672313 - 0.06875882333768812im
⋮
-0.09443848623560769 - 0.2338844220911809im
0.03876180415542871 - 0.1046668256453935im
-0.061083232690649136 - 0.031837699478320845im
0.30035443803713063 + 0.1058799366579733im
-0.08651495842681041 + 0.023266804247792948im
-0.04426540139394594 - 0.09533326446033662im
-0.10966018436017433 + 0.09960858051674291im
-0.09853968652494437 - 0.10750754555361194im
-0.06044076121243973 + 0.06160842524982186im
0.11790585486419344 + 0.021114930415067075im
-0.05791997418139597 - 0.011304768297034916im
0.010755930619856897 + 0.21570364028995265im
No obstante..
(0.3ψ₂ + 2ψ₃)/2 |> isnormalized
false
Notamos que este nuevo estado no se normaliza por defecto. La Normalización es una condición requerida para los estados puros del sistema finito dimensional (como es nuestro caso. En casos más generales de sistemas cuánticos, esta condición se traduce a que el mapa lineal de densidad sea tipo traza con traza igual a 1).
Es decir, requerimos que la norma de la representación pura del estado (aquí denotados como \(\psi\)) sea igual a 1. Debemos siempre recordar que posterior a alguna operación, debemos normalizar de nuevo el vector representante del estado.
ψ₄ = (0.3ψ₂ + 2ψ₃)/2
ArrayReg{1, Complex{Float64}, Array...}
active qubits: 5/5
ψ₄ |> normalize! |> isnormalized
true
Exploramos ahora la norma:
ψ₄' * ψ₄ ## la comilla ' representa la operación de transposición en la base selecta.
1.0 + 0.0im
Compuertas lógicas y mediciones¶
Mediciones¶
Las compuertas lógicas son la forma en que podemos transformar los estados de los registros de qubits que hemos creados. En Yao estos se pueden definir, al igual que los aparatos de medición, en los denominados bloques.
Primero, preparemos un registro con la suma de dos registros y lo normalizamos posteriormente:
r = normalize!(ArrayReg(bit"000") + ArrayReg(bit"111"))
ArrayReg{1, Complex{Float64}, Array...}
active qubits: 3/3
r.state
8×1 Array{Complex{Float64},2}:
0.7071067811865475 + 0.0im
0.0 + 0.0im
0.0 + 0.0im
0.0 + 0.0im
0.0 + 0.0im
0.0 + 0.0im
0.0 + 0.0im
0.7071067811865475 + 0.0im
Medir este registro es tan sencillo como utilizar el operador pipe, “pasándole” el registro al bloque de medición, en este caso, de tres qubits.
r |> Measure(3)
Measure(3)
Recordemos que en mecánica cuántica, el acto de permitir que el sistema cuántico aislado interactue con un ambiente de baja coherencia resulta en perder la superposición que antes teníamos y obtener un solo estado bien definido.
Los detalles de cómo sucede esto es, en general, aun un problema abierto conocido como el problema de medición, siendo aun uno de los misterios más importantes a resolver en los fundamentos teóricos de la mecánica cuántica
r.state
8×1 Array{Complex{Float64},2}:
0.0 + 0.0im
0.0 + 0.0im
0.0 + 0.0im
0.0 + 0.0im
0.0 + 0.0im
0.0 + 0.0im
0.0 + 0.0im
1.0 + 0.0im
Notamos que el estado mostrado ha colapsado de ser uan superposición a representar un estado con análogo clásico que se puede entender como un resultado definido.
Esto fue un ejemplo de un bloque. Los bloques consisten de operaciones generales como medición o compuertas lógicas, pero igualmente Yao nos permite realizar el proceso de medición sin tener que utilizar bloques. La mayoría de transformaciones tienen su versión fuera de bloque:
## Mostrará un resultado distinto si se sigue midiendo...
(product_state(5, 0b10) + product_state(5, 0b11)) |> measure
1-element Array{BitBasis.BitStr{5,Int64},1}:
00010 ₍₂₎
Podemos también especificar el número de veces que quisieramos medir:
reg = rand_state(7)
ArrayReg{1, Complex{Float64}, Array...}
active qubits: 7/7
measure(reg; nshots=5)
5-element Array{BitBasis.BitStr{7,Int64},1}:
1110111 ₍₂₎
1110010 ₍₂₎
1100101 ₍₂₎
0010111 ₍₂₎
1111111 ₍₂₎
Compuertas comunes¶
Las compuertas lógicas, fuera de bloques, son representados por sus símbolos comunes para las más utilizadas:
typeof((X, Z, Y, H))
Tuple{XGate,ZGate,YGate,HGate}
donde sus matrices unitarias asociadas en la base canónica son:
mat(X)
2×2 LuxurySparse.PermMatrix{Complex{Float64},Int64,Array{Complex{Float64},1},Array{Int64,1}}:
0.0+0.0im 1.0+0.0im
1.0+0.0im 0.0+0.0im
mat(Y)
2×2 LuxurySparse.PermMatrix{Complex{Float64},Int64,Array{Complex{Float64},1},Array{Int64,1}}:
0.0+0.0im 0.0-1.0im
0.0+1.0im 0.0+0.0im
mat(Z)
2×2 LinearAlgebra.Diagonal{Complex{Float64},Array{Complex{Float64},1}}:
1.0+0.0im ⋅
⋅ -1.0+0.0im
mat(H)
2×2 Array{Complex{Float64},2}:
0.707107+0.0im 0.707107+0.0im
0.707107+0.0im -0.707107+0.0im
No obstante, nos enfocaremos en el uso dentro de bloques. Para hacer uso de ellos en bloques, debemos especificar cuántas y cuáles compuertas estarán dentro del bloque dado. Utilizamos repeat para repetir una compuerta n veces.
Como ejemplo, considere el siguiente estado:
ArrayReg(bit"0").state
2×1 Array{Complex{Float64},2}:
1.0 + 0.0im
0.0 + 0.0im
(ArrayReg(bit"0") |> repeat(1, X)).state
2×1 Array{Complex{Float64},2}:
0.0 + 0.0im
1.0 + 0.0im
(ArrayReg(bit"0") |> repeat(2, X)).state
2×1 Array{Complex{Float64},2}:
1.0 + 0.0im
0.0 + 6.94608316725543e-310im
La compuerta \(X\) de pauli se conoce como el bit flip que, como se muestra arriba, transforma el estado \(|0\rangle\) hacia \(|1\rangle\) y viceversa. Esto significa que al aplicarla dos veces, regresamos al estado original en este caso.
Para una lista más detallada y efecto de las compuertas más utlizadas ver aquí.
Aquí se está operando unqubit individual con una cantidad general \(n\) de compuertas secuenciales. Otra forma importante de operar es especificar la accion en un registro de \(m\) qubits con compuertas presentar en solamente algunos de los qubits. Considere:
mat(put(3, 2=>X))
8×8 LuxurySparse.PermMatrix{Complex{Float64},Int64,Array{Complex{Float64},1},Array{Int64,1}}:
0.0+0.0im 0.0+0.0im 1.0+0.0im … 0.0+0.0im 0.0+0.0im 0.0+0.0im
0.0+0.0im 0.0+0.0im 0.0+0.0im 0.0+0.0im 0.0+0.0im 0.0+0.0im
1.0+0.0im 0.0+0.0im 0.0+0.0im 0.0+0.0im 0.0+0.0im 0.0+0.0im
0.0+0.0im 1.0+0.0im 0.0+0.0im 0.0+0.0im 0.0+0.0im 0.0+0.0im
0.0+0.0im 0.0+0.0im 0.0+0.0im 0.0+0.0im 1.0+0.0im 0.0+0.0im
0.0+0.0im 0.0+0.0im 0.0+0.0im … 0.0+0.0im 0.0+0.0im 1.0+0.0im
0.0+0.0im 0.0+0.0im 0.0+0.0im 0.0+0.0im 0.0+0.0im 0.0+0.0im
0.0+0.0im 0.0+0.0im 0.0+0.0im 1.0+0.0im 0.0+0.0im 0.0+0.0im
el comando put(m, k=>C) coloca la compuerta C en el qubit k en el registro con m qubits (siendo k<m). Esto se representa como una matriz sobre el espacio vectorial del registro entero. Para poder enlazar varios bloques put, utilizamos chain para crear una cadena de bloques
chain(put(3, 2=>X), put(3, 1=>Y))
nqubits: 3
chain
├─ put on (2)
│ └─ X
└─ put on (1)
└─ Y
La cadena tiene una estructura de árbol que nos permite acceder a cada etapa como si fuese un arreglo (pues es efectivamente un subtipo de arreglo abstracto en Julia):
chain(put(3, 2=>X), put(3, 1=>Y))[2]
nqubits: 3
put on (1)
└─ Y
La matriz asociada a la cadena será, de nuevo, un operador unitario sobre el espacio vectorial asociado a todo el registro activo:
mat(chain(put(3, 2=>X), put(3, 1=>Y)))
8×8 LuxurySparse.PermMatrix{Complex{Float64},Int64,Array{Complex{Float64},1},Array{Int64,1}}:
0.0+0.0im 0.0+0.0im 0.0+0.0im … 0.0+0.0im 0.0+0.0im 0.0+0.0im
0.0+0.0im 0.0+0.0im 0.0+1.0im 0.0+0.0im 0.0+0.0im 0.0+0.0im
0.0+0.0im 0.0-1.0im 0.0+0.0im 0.0+0.0im 0.0+0.0im 0.0+0.0im
0.0+1.0im 0.0+0.0im 0.0+0.0im 0.0+0.0im 0.0+0.0im 0.0+0.0im
0.0+0.0im 0.0+0.0im 0.0+0.0im 0.0+0.0im 0.0+0.0im 0.0-1.0im
0.0+0.0im 0.0+0.0im 0.0+0.0im … 0.0+0.0im 0.0+1.0im 0.0+0.0im
0.0+0.0im 0.0+0.0im 0.0+0.0im 0.0-1.0im 0.0+0.0im 0.0+0.0im
0.0+0.0im 0.0+0.0im 0.0+0.0im 0.0+0.0im 0.0+0.0im 0.0+0.0im
Compuertas de control¶
El diagrama mostrado al inicio del documento tenía elementos que conectan dos lineas de evolución de qubits. Estas son compuertas de control que consisten de un qubit de control y otro de respuesta.
El qubit de control debe estar en el estado \(|1\rangle\) para que el qubit de respuesta aplique la compuerta especificada. Es decir, tenemos versiones de las compuertas discutidas anteriormente que contienen un control: Control-\(X\), control-\(H\), etc.
Cabe agregar que aquí es donde comienzan a surgir efectos interesantes que contrastan el cómputo cuántico de el cómputo clásico, pues puede ser el caso que un qubit colapse al estado \(|1\rangle\) con cierta probabilidad \(\alpha <1\).
Esta propiedad se explota en algoritmos cuánticos para cargar información probabilística condicional que nos pueda garantizar encontrar lo que deseamos con menor cómputo de lo que condicionales clásicos requerirían.
control(4, 3, 1 => X)
nqubits: 4
control(3)
└─ (1,) X
El anterior comando crea una compuerta de control \(X\) en un registro de tamaño \(4\), con qubit de control \(3\) y qubit de respuesta \(1\). Es decir, solamente si el qubit \(3\) resulta tener el estado \(|1\rangle\) vamos a actuar con \(X\) sobre \(1\).
Es importante notar que el estado de \(3\) va a ser conocido hasta que realicemos la medición al final del circuito (o que se rompa la coherencia cuántica con otras interacciones con el ambiente, pero de manera ideal, sería mediante la medición controlada). Esto quiere decir que el efecto de \(X\) sobre \(1\) es probabilístico también, y no sabremos si se efectuó hasta medir (y a veces ni midiendo sabremos si un efecto particular se dio a cabo dentro de un circuito complejo).
Aplicando bloques a registros¶
Apliquemos todo lo anteriormente visto para crear nuestro primer circuito cuántico.
using YaoBase: rand_unitary ## Genera matrices unitarias de manera aleatorio
circuit = chain(5,
control(5, 3=>Rx(0.25π)),
put(5, (2,3)=>GeneralMatrixBlock(rand_unitary(4))),
swap(5, 3, 4),
repeat(5, H, 2:5),
put(5, 2=>Ry(0.6)))
nqubits: 5
chain
├─ control(5)
│ └─ (3,) rot(X, 0.7853981633974483)
├─ put on (2, 3)
│ └─ matblock(...)
├─ put on (3, 4)
│ └─ SWAP
├─ repeat on (2, 3, 4, 5)
│ └─ H
└─ put on (2)
└─ rot(Y, 0.6)
Aquí vemos una cadena de bloques para actuar en un registro de 5 qubits activos. En orden se describen a continuación:
Bloque de control de un operador de rotación (respecto al eje \(x\)) de fase \(\pi/4\), controlado por el qubit 5 y respondiendo hacia el qubit 3 (notemos que no le ocupamos pasar el número de registros, pues estamos utilizando un constructor especial de
controlque utiliza lazy evaluation)Una matriz general unitaria siendo ejecutada como compuerta lógica hacia los qubits \(2\) y \(3\). Observe que la matriz es de rango \(4=2^2\), por lo que actúa en pares de qubits.
Una acción de intercambio de qubits. El qubit \(3\) y \(4\) han sido intercambiados de índice.
Un bloque de compuertas de Hadamard, \(H\), aplicadas en los qubits \(2, 3\), y \(4\).
Una rotación de fase de 0.6 radianes respecto al eje \(y\)
Las rotaciones aquí mencionadas son respecto a los ejes espaciales definidos con el modelo de esfera de Block.
Para aplicar este circuito a algún registro utilizamos el comando apply!:
result = apply!(zero_state(5), circuit)
ArrayReg{1, Complex{Float64}, Array...}
active qubits: 5/5
result.state
32×1 Array{Complex{Float64},2}:
-0.14987858288484762 + 0.09923372408483917im
0.0 + 0.0im
0.03620111373867382 + 0.07381850225238377im
0.0 + 0.0im
-0.14987858288484762 + 0.09923372408483917im
0.0 + 0.0im
0.03620111373867382 + 0.07381850225238377im
0.0 + 0.0im
-0.34895255831203204 - 0.012533560792136647im
0.0 + 0.0im
-0.07374217709281457 + 0.28907870849467243im
0.0 + 0.0im
-0.34895255831203204 - 0.012533560792136647im
⋮
-0.14987858288484762 + 0.09923372408483917im
0.0 + 0.0im
0.03620111373867382 + 0.07381850225238377im
0.0 + 0.0im
-0.34895255831203204 - 0.012533560792136647im
0.0 + 0.0im
-0.07374217709281457 + 0.28907870849467243im
0.0 + 0.0im
-0.34895255831203204 - 0.012533560792136647im
0.0 + 0.0im
-0.07374217709281457 + 0.28907870849467243im
0.0 + 0.0im
Podemos explorar el caso de un registro donde no todos los qubits están activos y utilizar una notación más elegante utilizando Pipe:
using Pipe
@pipe zero_state(10) |> focus!(1:5) |> apply!(_, circuit) |> state
32×32 Array{Complex{Float64},2}:
-0.149879+0.0992337im 0.0+0.0im … 0.0+0.0im 0.0+0.0im 0.0+0.0im
0.0+0.0im 0.0+0.0im 0.0+0.0im 0.0+0.0im 0.0+0.0im
0.0362011+0.0738185im 0.0+0.0im 0.0+0.0im 0.0+0.0im 0.0+0.0im
0.0+0.0im 0.0+0.0im 0.0+0.0im 0.0+0.0im 0.0+0.0im
-0.149879+0.0992337im 0.0+0.0im 0.0+0.0im 0.0+0.0im 0.0+0.0im
0.0+0.0im 0.0+0.0im … 0.0+0.0im 0.0+0.0im 0.0+0.0im
0.0362011+0.0738185im 0.0+0.0im 0.0+0.0im 0.0+0.0im 0.0+0.0im
0.0+0.0im 0.0+0.0im 0.0+0.0im 0.0+0.0im 0.0+0.0im
-0.348953-0.0125336im 0.0+0.0im 0.0+0.0im 0.0+0.0im 0.0+0.0im
0.0+0.0im 0.0+0.0im 0.0+0.0im 0.0+0.0im 0.0+0.0im
-0.0737422+0.289079im 0.0+0.0im … 0.0+0.0im 0.0+0.0im 0.0+0.0im
0.0+0.0im 0.0+0.0im 0.0+0.0im 0.0+0.0im 0.0+0.0im
-0.348953-0.0125336im 0.0+0.0im 0.0+0.0im 0.0+0.0im 0.0+0.0im
⋮ ⋱ ⋮
-0.149879+0.0992337im 0.0+0.0im … 0.0+0.0im 0.0+0.0im 0.0+0.0im
0.0+0.0im 0.0+0.0im 0.0+0.0im 0.0+0.0im 0.0+0.0im
0.0362011+0.0738185im 0.0+0.0im 0.0+0.0im 0.0+0.0im 0.0+0.0im
0.0+0.0im 0.0+0.0im 0.0+0.0im 0.0+0.0im 0.0+0.0im
-0.348953-0.0125336im 0.0+0.0im 0.0+0.0im 0.0+0.0im 0.0+0.0im
0.0+0.0im 0.0+0.0im … 0.0+0.0im 0.0+0.0im 0.0+0.0im
-0.0737422+0.289079im 0.0+0.0im 0.0+0.0im 0.0+0.0im 0.0+0.0im
0.0+0.0im 0.0+0.0im 0.0+0.0im 0.0+0.0im 0.0+0.0im
-0.348953-0.0125336im 0.0+0.0im 0.0+0.0im 0.0+0.0im 0.0+0.0im
0.0+0.0im 0.0+0.0im 0.0+0.0im 0.0+0.0im 0.0+0.0im
-0.0737422+0.289079im 0.0+0.0im … 0.0+0.0im 0.0+0.0im 0.0+0.0im
0.0+0.0im 0.0+0.0im 0.0+0.0im 0.0+0.0im 0.0+0.0im
Esto muestra el flujo completo del circuito, desde el registro, hasta la medición de su estado final.
Métricas de comparación de registros¶
Posterior a la medición u operación de compuerta lógica hacia un registro, nos puede gustar verificar la fidelidad con la cual el estado cuántico corresponde al que esperamos de manera teórica. En la práctica, dentro de una computadora cuántica, esta fidelidad se ve comprometida en cada operación que realizamos, así como la evolución natural del sistema.
Algunas de estas métricas ya están implementadas en Yao:
fidelity(rand_state(6), rand_state(6))
0.015114896727965663
Ésta es calculada con la fórmula \( {\displaystyle F(\rho ,\sigma )=\left(\operatorname {tr} {\sqrt {{\sqrt {\rho }}\sigma {\sqrt {\rho }}}}\right)^{2}}\).
Donde \(\rho\) y \(\sigma\) son los estados del sistema (pensados en generalidad como operadores de densidad y no como su forma pura como vectores). También tenemos la distancia inducida por la traza en el espacio de estos operadores tipo traza. Éste se define como \(\frac{1}{2} || \rho- \sigma||_{\text{tr}}\) y se utiliza como tracedist:
tracedist(rand_state(6), rand_state(6))
1-element Array{Float64,1}:
1.9989601608188385
Ambos métricas mostradas utilizan el operador de densidad general del estado, pero al estar considerando solamente sistemas de dimensión finita, podemos representar sin ambigüedad esta en una matriz de densidad de la siguiente forma:
(rand_state(1) |> ρ).state
2×2×1 Array{Complex{Float64},3}:
[:, :, 1] =
0.0785373+0.0im 0.268467+0.017163im
0.268467-0.017163im 0.921463+0.0im
Algorítmica¶
Transformada cuántica de Fourier¶
Como ejemplo de un algoritmo cuántico clásico, construiremos el circuito asociado con la transformada cuántica de Fourier. Este es un algoritmo que equivale a realizar la transformada inversa discreta de Fourier a una cadena de bits, pero utilizando un circuito del tipo que acabamos de construir.
Los detalles teóricos profundos serán omitidos dada la disponibilidad grande que hay de recursos que ya lo explican. Considere el siguiente diagrama que representa el circuito/algoritmo:
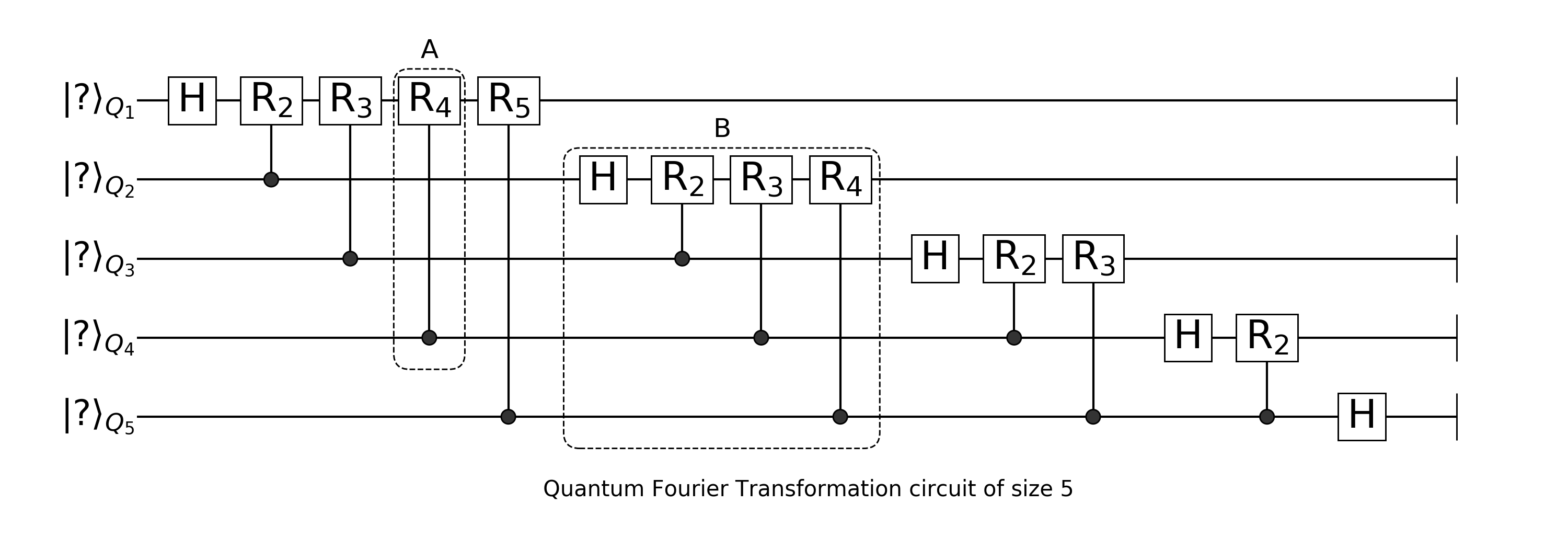
Este muestra el caso para un registro de \(5\) qubits, no obstante, programaremos el caso general para un registro de \(n\) qubits. El diagrama sugiere que una forma ordenada de programar este circuito es aprovechar su estructura repetitiva.
Tenemos el bloque A definido por una compuerta de rotación controlada cuya posición en la cadena es determinada por cuál es su qubit de control y de respuesta, así como el valor de su rotación. Estos son respectivamente i, j, y k.
A(i::Int, j::Int, k::Int) = control(i, j=>shift(2π/(1<<k)))
A (generic function with 1 method)
El bloque B que está compuesto por el patrón de \(\{H, R_2, \dots, R_{n-i+1}\}\) donde \(i\) es el índice del qubit respuesta donde es aplicado B y \(n\) es el número total de qubits.
B(n::Int, i::Int) = chain(i==j ? kron(i=>H) : A(j, i, j-i+1) for j = i:n)
B (generic function with 1 method)
Finalmente, el algoritmo de QFT (Quantum Fourier Transform) es definido por una cadena sencilla de bloques B.
QFT(n::Int) = chain(n, B(n, i) for i = 1:n)
QFT (generic function with 1 method)
Así, acabamos de programar la versión general del circuito de QFT:

Aquí vemos el caso con \(n = 4\).
QFT(4)
nqubits: 4
chain
├─ chain
│ ├─ kron
│ │ └─ 1=>H
│ ├─ control(2)
│ │ └─ (1,) shift(1.5707963267948966)
│ ├─ control(3)
│ │ └─ (1,) shift(0.7853981633974483)
│ └─ control(4)
│ └─ (1,) shift(0.39269908169872414)
├─ chain
│ ├─ kron
│ │ └─ 2=>H
│ ├─ control(3)
│ │ └─ (2,) shift(1.5707963267948966)
│ └─ control(4)
│ └─ (2,) shift(0.7853981633974483)
├─ chain
│ ├─ kron
│ │ └─ 3=>H
│ └─ control(4)
│ └─ (3,) shift(1.5707963267948966)
└─ chain
└─ kron
└─ 4=>H
qft = QFT(4); iqft = QFT(4)';
@pipe product_state(bit"0110") |> apply!(_, qft) |> state
16×1 Array{Complex{Float64},2}:
0.24999999999999992 + 0.0im
-0.17677669529663678 + 0.17677669529663684im
-1.530808498934191e-17 - 0.24999999999999992im
0.17677669529663684 + 0.17677669529663678im
-0.24999999999999992 + 0.0im
0.17677669529663678 - 0.17677669529663684im
1.530808498934191e-17 + 0.24999999999999992im
-0.17677669529663684 - 0.17677669529663678im
0.24999999999999992 + 0.0im
-0.17677669529663678 + 0.17677669529663684im
-1.530808498934191e-17 - 0.24999999999999992im
0.17677669529663684 + 0.17677669529663678im
-0.24999999999999992 + 0.0im
0.17677669529663678 - 0.17677669529663684im
1.530808498934191e-17 + 0.24999999999999992im
-0.17677669529663684 - 0.17677669529663678im
Estimación de fase¶
El algoritmo de transformada de Fourier se utiliza como una subrutina en muchos otros algoritmos. Uno de ellos es otro algoritmo básico famoso phase estimation (estimación de fase) que nos permite resolver el siguiente problema:
Sea \(U\) una matriz unitaria y sea \(v\) un vector propio de \(U\), es decir, se cumple que \(Uv = e^{2\pi i \theta} v\) para algún \(\theta\). Queremos estimar el valor de \(\theta\) para un \(U\) y \(v\) fijos.
El algoritmo de estimación de fase estima \(\theta\) con alta probabilidad (un término técnico en algoritmos probabilísticos que significa que aumentando el tamaño muestral nos acercamos en el límite a probabilidad 1 de estar correctos) con un número de qubits que solo ocupa crecer como \(O(\log(1/\epsilon))\) donde el error aditivo es \(\epsilon\).
Considere el siguiente diagrama:
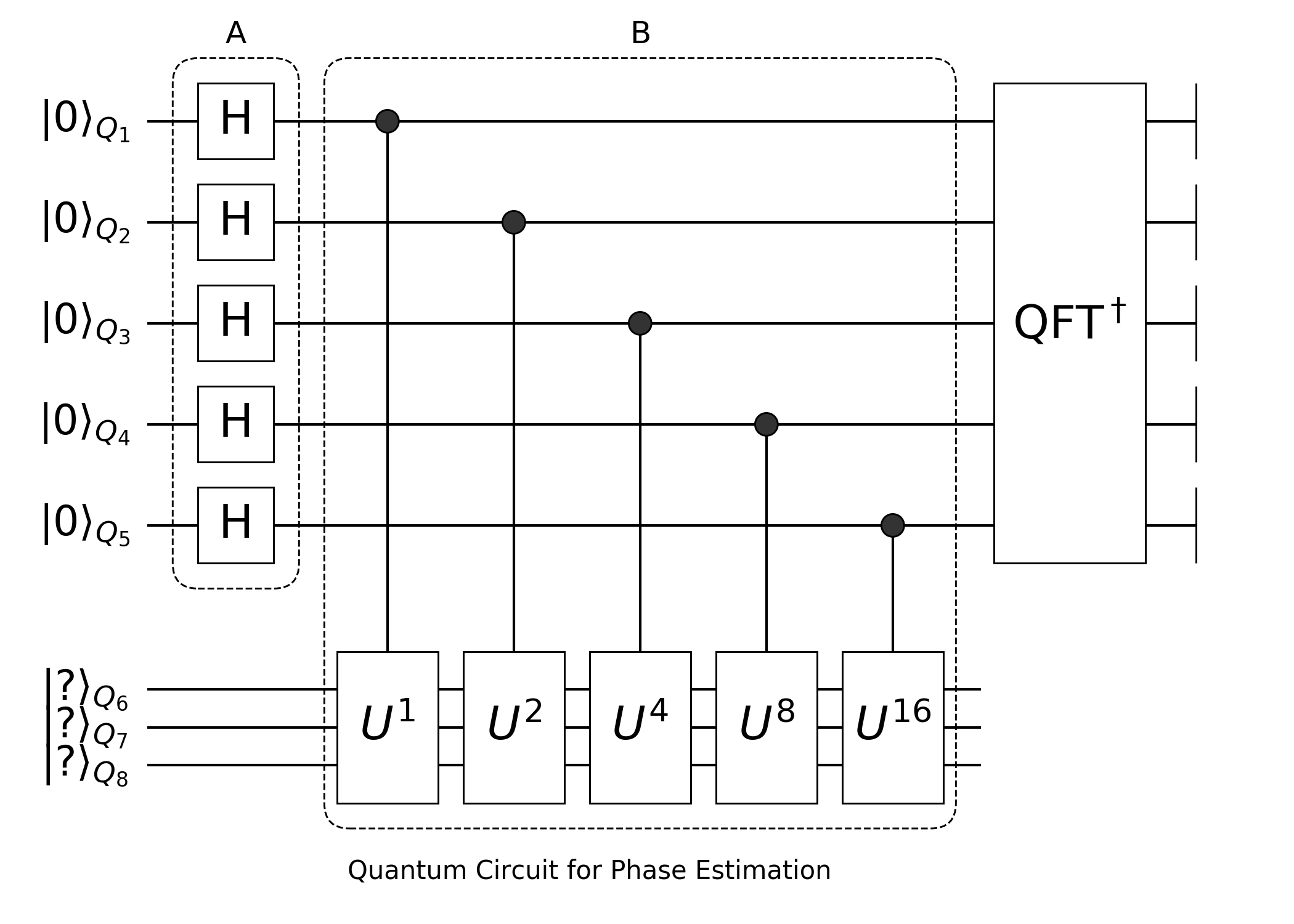
Notemos que aquí tenemos dos conjuntos independientes de registros, los primeros que van a ser transformados por las compuertas de hadamard y QFT. Éstos controlan el segundo registro, que consiste en el estado \(v\) y una sucesión de aplicaciones de poderes de \(U\) para extraer así fases múltiple de la que estamos buscando, lo cual nos servirá para estimar correctamente \(\theta\).
Definamos la cadena de bloques que define la sucesión de poderes de \(U\).
ControlU(n, m, U) = chain(n+m,
control(k, n+1:n+m => matblock(U^(2^(k-1))))
for k in 1:n)
ControlU (generic function with 1 method)
Luego, crear el algoritmo del circuito arriba mostrado es tan sencillo como:
PE(n, m, U) =chain(n+m, ## Número total de qubits, sumando ambos registros.
concentrate(Hadamards(n), 1:n), ## H en el primer registro.
ControlU(n, m, U),
concentrate(QFT(n)', 1:n))
PE (generic function with 1 method)
Este algoritmo es utilizado también como base o subrutina de otros algoritmos clásicos, por ejemplo el algoritmo de Shor para factorización de números enteros.
